4章 ニューラルネットワークの学習
本章のテーマは、ニューラルネットワークの学習です。
~
4.1 データから学習する
4.1.1 データ駆動
4.1.2 訓練データとテストデータ
4.2 損失関数
4.2.1 2乗和誤差
損失関数として用いられる関数はいくつかありますが、もっとも有名ななものは2乗和誤差(sum of squared error)でしょう。
~
julia> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0];
julia> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0];
~
function sum_squared_error(y, t)
return 0.5 * sum((y-t).^2)
end
~
julia> # 「3」を正解とする
julia> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0];
julia>
julia> # 例1:「3」の確率が最も高い場合(0.6)
julia> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0];
julia> sum_squared_error(y, t)
0.09750000000000003
julia>
julia> # 例1:「7」の確率が最も高い場合(0.6)
julia> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0];
julia> sum_squared_error(y, t)
0.5974999999999999
ここでは2つの例を示しています。
~
4.2.2 交差エントロピー誤差
2乗和誤差と別の損失関数として、交差エントロピー誤差(cross entropy error)もよく用いられます。
~
julia> function cross_entropy_error(y, t)
delta = 1.e-7
return -sum(t .* log.(y .+ delta))
end
cross_entropy_error (generic function with 1 method)
~
julia> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0];
julia> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0];
julia> cross_entropy_error(y, t)
0.510825457099338
julia>
julia> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0];
julia> cross_entropy_error(y, t)
2.302584092994546
~
4.2.3 ミニバッチ処理
~
include("dataset/mnist.jl")
import .MNIST: load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=true, one_hot_label=true)
print(size(x_train)) # (60000, 784)
print(size(t_train)) # (60000, 10)
~
それでは、この訓練データの中からランダムに10枚だけ抜き出すには、どうすればよいのでしょうか?
~
import Random: shuffle
train_size = size(t_train, 1)
batsh_size = 10
batch_mask = shuffle(1:train_size)[1:batch_size]
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
~
julia> import Random: shuffle
julia> shuffle(1:60000)[1:10]
10-element Vector{Int64}:
8130
17124
36096
52441
21595
23334
25369
46353
52087
6978
4.2.4 [バッチ対応版] 交差エントロピー誤差の実装
では、ミニバッチのようなデータに対応した交差エントロピー誤差はどのように実装できるでしょうか?
これは、先ほど実装した交差エントロピー誤差──それはひとつのデータを対象とした誤差でした──を改良することで簡単に実装できます。
ここでは、データがひとつの場合と、データがバッチとしてまとめられて入力される場合の両方のケースを多重ディスパッチで実装します。
julia> function cross_entropy_error(y::Vector{T}, t) where T
delta = 1.e-7
return -sum(t .* log.(y .+ delta))
end
cross_entropy_error (generic function with 1 method)
julia> function cross_entropy_error(y::Matrix{T}, t) where T
batch_size = size(y, 1)
return sum(cross_entropy_error.([y[i,:] for i=1:batch_size], [t[i,:] for i=1:batch_size])) / batch_size
end
cross_entropy_error (generic function with 2 methods)
~
また、教師データがラベルとして与えられたとき(one-hot表現ではなく、「2」や「7」といったラベルとして与えられたとき)、交差エントロピー誤差は次のように実装することができます。
function cross_entropy_error(y::Vector{T}, t::Y) where T <: Real where Y <: Integer
delta = 1.e-7
return -log.(y[t] .+ delta)
end
function cross_entropy_error(y::Matrix{T}, t::Vector{Y}) where T <: Real where Y <: Integer
batch_size = size(y, 1)
return sum(cross_entropy_error.([y[i,:] for i=1:batch_size], [t[i] for i=1:batch_size])) / batch_size
end
実装のポイントは、one-hot表現でtが0の要素は、交差エントロピー誤差も0であるから、その計算は無視してもよいということです。
~
4.2.5 なぜ損失関数を設定するのか?
~
4.3 数値微分
4.3.1 微分
~
# 悪い実装例
function numerical_diff(f, x)
h = 1e-50
return (f(x+h) - f(x)) / h
end
~
julia> Float32(10e-50)
0.0f0
~
function numerical_diff(f, x)
h = 1e-4
return (f(x+h) - f(x-h)) / 2h
end
4.3.2 数値微分の例
~
function function_1(x)
return 0.01x^2 + 0.1x
end
続いてこの関数を描画します。
~
using Plots
x = 0:0.1:20
y = function_1.(x)
plot(xlabel="x", ylabel="f(x)", leg=false)
plot!(x, y)
~
julia> numerical_diff(function_1, 5)
0.1999999999990898
julia> numerical_diff(function_1, 10)
0.2999999999986347
4.3.3 偏微分
~
function function_2(x)
return x[0]^2 + x[1]^2
# または return sum(x.^2)
end
~
問1:x0=3、x1=4のときのx0に対する偏微分を求めよ。
julia> function function_tmp1(x0)
return x0^2 + 4.0^2
end
function_tmp1 (generic function with 1 method)
julia> numerical_diff(function_tmp1, 3.0)
6.00000000000378
問2:x0=3、x1=4のときのx1に対する偏微分を求めよ。
julia> function function_tmp2(x1)
return 3.0^2 + x1^2
end
function_tmp2 (generic function with 1 method)
julia> numerical_diff(function_tmp2, 4.0)
7.999999999999119
これらの問題では、変数がひとつだけの関数を定義して、その関数について微分を求めるような実装を行っています。
~
4.4 勾配
先の例では、x0とx1の偏微分の計算を変数ごとに計算しました。
~
function numerical_gradient(f, x)
h = 1e-4 # 0.0001
grad = zero(x) # xと同じ形状の配列を生成
for idx = 1:size(x,1)
tmp_val = x[idx]
# f(x+h) の計算
x[idx] += h
fxh1 = f(x)
# f(x-h) の計算
x[idx] -= 2h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / 2h
x[idx] = tmp_val # 値を元に戻す
end
return grad
end
~
julia> numerical_gradient(function_2, [3.0, 4.0])
2-element Vector{Float64}:
5.9999999999860165
7.999999999999119
julia> numerical_gradient(function_2, [0.0, 2.0])
2-element Vector{Float64}:
0.0
3.9999999999995595
julia> numerical_gradient(function_2, [3.0, 0.0])
2-element Vector{Float64}:
5.999999999994898
0.0
~
4.4.1 勾配法
~
function gradient_descent(f, init_x; lr=0.01, step_num=100)
x = init_x
for i = 1:step_num
grad = numerical_gradient(f, x)
x .-= lr * grad
end
return x
end
引数のfは最適化したい関数、init_xは初期値、lrはlearning rateを意味する学習率、step_numは勾配法による繰り返しの数とします。
~
問:f(x0,x1)=x0^2+x1^2の最小値を勾配法で求めよ。
julia> function function_2(x)
return x[0]^2 + x[1]^2
end
function_2 (generic function with 2 methods)
julia> init_x = [-3.0, 4.0]
2-element Vector{Float64}:
-3.0
4.0
julia> gradient_descent(function_2, init_x, lr=0.1, step_num=100)
2-element Vector{Float64}:
-6.111107929002627e-10
8.148143905330748e-10
~
# 学習率が大きすぎる例:lr=10.0
julia> init_x = [-3.0, 4.0];
julia> gradient_descent(function_2, init_x, lr=10.0, step_num=100)
2-element Vector{Float64}:
9.453764611121996e11
2.56007253831004e13
# 学習率が大きすぎる例:lr=1e-10
julia> init_x = [-3.0, 4.0];
julia> gradient_descent(function_2, init_x, lr=1e-10, step_num=100)
2-element Vector{Float64}:
-2.999999939999995
3.9999999199999934
4.4.2 ニューラルネットワークに対する勾配
ニューラルネットワークの学習においても、勾配を求める必要があります。
~
include("common/functions.jl")
include("common/gradient.jl")
import .Functions: softmax, cross_entropy_error
import .Gradient: numerical_gradient
struct SimpleNet
W::Matrix{T} where T <: AbstractFloat
end
SimpleNet() = SimpleNet(randn(2,3))
function predict(self::SimpleNet, x)
return x*self.W
end
function loss(self::SimpleNet, x, t)
z = predict(self, x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
end
~
julia> net = SimpleNet()
SimpleNet([0.8614474575097301 -1.0564545610725369 1.5079058577423168; 0.05480306208407878 0.15211432230030267 1.147686557481568])
julia> net = SimpleNet([0.47355232 0.9977393 0.84668094; 0.85557411 0.03563661 0.69422093])
SimpleNet([0.47355232 0.9977393 0.84668094; 0.85557411 0.03563661 0.69422093])
julia> net.W
2×3 Matrix{Float64}:
0.473552 0.997739 0.846681
0.855574 0.0356366 0.694221
julia>
julia> x = [0.6 0.9]
1×2 Matrix{Float64}:
0.6 0.9
julia> p = predict(net, x)
1×3 Matrix{Float64}:
1.05415 0.630717 1.13281
julia> argmax(p)
CartesianIndex(1, 3)
julia>
julia> t = [0.0 0.0 1.0]
1×3 Matrix{Float64}:
0.0 0.0 1.0
julia> loss(net, x, t)
0.9280682857864075
続いて、勾配を求めてみましょう。
~
julia> function f(W)
return loss(net, x, t)
end
f (generic function with 1 method)
julia> dW = numerical_gradient(f, net.W)
2×3 Matrix{Float64}:
0.219248 0.143562 -0.36281
0.328871 0.215344 -0.544215
~
なお、上の実装では、新しい関数を定義するために、「function f(x) …」のように書きましたが、Juliaではラムダ式という記法を使って書くこともできます。
たとえば、ラムダ式を使って次のように実装することもできます。
julia> f = (w)->loss(net, x, t)
#1 (generic function with 1 method)
julia> dW = numerical_gradient(f, net.W)
4.5 学習アルゴリズムの実装
4.5.1 2層ニューラルネットワークの構造体
include("common/functions.jl")
include("common/gradient.jl") # numerical_gradient
using .Functions
import .Gradient: numerical_gradient
mutable struct TwoLayerNet
params::Dict
end
function TwoLayerNet(input_size, hidden_size, output_size, weight_init_std=0.01)
params = Dict()
params["W1"] = weight_init_std * randn(input_size, hidden_size)
params["b1"] = zeros(1, hidden_size)
params["W2"] = weight_init_std * randn(hidden_size, output_size)
params["b2"] = zeros(1, output_size)
return TwoLayerNet(params)
end
function predict(self::TwoLayerNet, x)
W1, W2 = self.params["W1"], self.params["W2"]
b1, b2 = self.params["b1"], self.params["b2"]
a1 = x * W1 .+ b1
z1 = sigmoid.(a1)
a2 = z1 * W2 .+ b2
y = softmax(a2)
return y
end
# x:入力データ, t:教師データ
function loss(self::TwoLayerNet, x, t)
y = predict(self, x)
return cross_entropy_error(y, t)
end
function accuracy(self::TwoLayerNet, x, t)
y = self.predict(self, x)
y = argmax(y, dims=2)
t = argmax(t, dims=2)
accuracy = sum(y .== t) / size(x, 1)
return accuracy
end
# x:入力データ, t:教師データ
function numerical_gradient(self::TwoLayerNet, x, t)
loss_W = (W)->loss(self, x, t)
grads = Dict()
grads["W1"] = numerical_gradient(loss_W, self.params["W1"])
grads["b1"] = numerical_gradient(loss_W, self.params["b1"])
grads["W2"] = numerical_gradient(loss_W, self.params["W2"])
grads["b2"] = numerical_gradient(loss_W, self.params["b2"])
return grads
end
~
net = TwoLayerNet(784, 100,10)
size(net.params["W1"]) # (784, 100)
size(net.params["b1"]) # ( 1, 100)
size(net.params["W2"]) # (100, 10)
size(net.params["b2"]) # ( 1, 10)
~
x = rand(100,784) # ダミーの入力データ(100枚分)
y = predict(net,x)
~
x = rand(100,784) # ダミーの入力データ(100枚分)
t = rand(100,10) # ダミーの正解ラベル(100枚分)
grads = numerical_gradient(net, x, t) # 勾配を計算
size(grads["W1"]) # (784, 100)
size(grads["b1"]) # ( 1, 100)
size(grads["W2"]) # (100, 10)
size(grads["b2"]) # ( 1, 10)
~
4.5.2 ミニバッチ学習の実装
include("dataset/mnist.jl")
include("ch04/two_layer_net.jl")
import Random: shuffle
using Plots
import .MNIST: load_mnist
using .TwoLayerNet_ch04 # TwoLayerNet
# データの読み込み
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=true, one_hot_label=true)
train_loss_list = zeros(0)
# ハイパーパラメータ
iters_num = 10000
train_size = size(x_train, 1)
batch_size = 100
learning_rate = 0.1
network = TwoLayerNet(784, 50, 10)
for i in 0:iters_num
# ミニバッチの取得
batch_mask = shuffle(1:train_size)[1:batch_size]
x_batch = x_train[batch_mask, :]
t_batch = t_train[batch_mask, :]
# 勾配の計算
grad = numerical_gradient(network, x_batch, t_batch)
# grad = gradient(network, x_batch, t_batch)
# パラメータの更新
for key=("W1", "b1", "W2", "b2")
network.params[key] -= learning_rate * grad[key]
end
loss_val = loss(network, x_batch, t_batch)
append!(train_loss_list, loss_val)
end
4.5.3 テストデータで評価
include("dataset/mnist.jl")
include("ch04/two_layer_net.jl")
import Random: shuffle
using Plots
import .MNIST: load_mnist
using .TwoLayerNet_ch04 # TwoLayerNet
# データの読み込み
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=true, one_hot_label=true)
train_loss_list = zeros(0)
train_acc_list = zeros(0)
test_acc_list = zeros(0)
# ハイパーパラメータ
iters_num = 10000
train_size = size(x_train, 1)
batch_size = 100
learning_rate = 0.1
network = TwoLayerNet(784, 50, 10)
# 1エポックあたりの繰り返し数
iter_per_epoch = max(train_size / batch_size, 1)
for i in 0:iters_num
batch_mask = shuffle(1:train_size)[1:batch_size]
x_batch = x_train[batch_mask, :]
t_batch = t_train[batch_mask, :]
# 勾配の計算
grad = numerical_gradient(network, x_batch, t_batch)
# grad = gradient(network, x_batch, t_batch)
# パラメータの更新
for key=("W1", "b1", "W2", "b2")
network.params[key] -= learning_rate * grad[key]
end
loss_val = loss(network, x_batch, t_batch)
append!(train_loss_list, loss_val)
# 1エポックごとに認識精度を計算
if i % iter_per_epoch == 0
train_acc = accuracy(network, x_train, t_train)
test_acc = accuracy(network, x_test, t_test)
append!(train_acc_list, train_acc)
append!(test_acc_list, test_acc)
println("train acc, test acc | $train_acc, $test_acc")
end
end
~
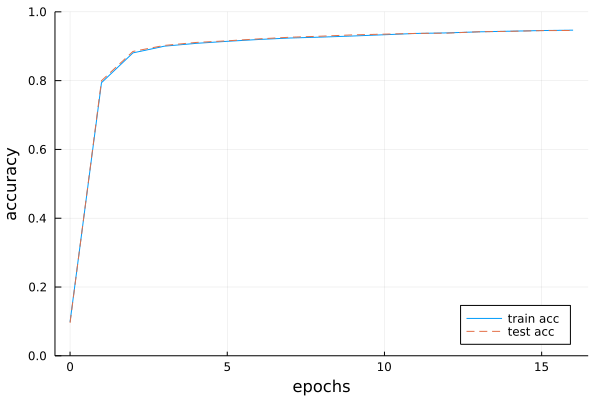
図4-12 訓練データとテストデータに対する認識精度の推移。横軸はエポック